Vectores.

 Vectores.

En un plano Bidimensional es un par ordenado de números reales (a1, a2...), en un espacio tridimensional es una terna ordenada de numeros reales (a1,a2,a3...).

Concepto geométrico de Vector

Es un segmento rectilíneo de módulo, dirección y sentido.

Los elementos de un vector pueden ser n° reales. Un vector se representa como V= (X1,X2,X3,...,Xn), donde X1,X2,X3,...,Xn se denominan componentes del vector.

Igualdad de Vectores.

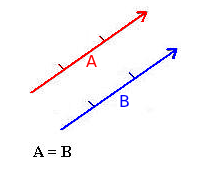
Dos vectores son iguales si tienen la misma dirección, el mismo sentido y la misma longitud. Tienen una misma dirección cuando están sobre la misma recta o sobre rectas paralelas. El sentido está determinado por una flecha.

Operaciones con Vectores.

1. Suma de Vectores: para poder sumar vectores estos deben permanecer al mismo espacio en donde se suman componente por componente. Entonces la suma de vectores está definida de la siguiente manera. V= (X1,X2,X3,...,Xn)    W= (Y1,Y2,Y3,...,Yn). V + W= (X1+Y1,X2+Y2,X3+Y3,...,Xn+Yn).
2. Multiplicación por un Escalar: se realiza multiplicando cada componente por el escalar (escalar=número cualquiera). Sea V un vector definido por V= (X1,X2,X3,...,Xn) y K un número cualquiera entonces. K . V= (K.X1,K.X2,K.X3,...,K.Xn).
3. Diferencia entre Vectores (Resta): para la resta de vectores, estos deben permanecer al mismo espacio y luego se procede a estar los componentes correspondientes. Sea V  y W dos vectores definidos por V= (X1,X2,X3,...Xn)       W= (Y1,Y2,Y3,...,Yn). Entonces la diferencia de vectores está definido de la siguiente manera; V - W= (X1-Y1,X2-Y2,X3-Y3,...,Xn-Yn).
4. Producto de Vectores: Es un escalar que se obtiene sumando los productos de los componentes entre sí. Sean los vectores V= (X1,X2,X3,...Xn)    y  W= (Y1,Y2,Y3,...,Yn) el producto se define de la siguiente manera V . W= (X1.Y1 + X2.Y2 + X3.Y3 + ... + Xn.Yn).

Conceptos Básicos. 

1. Vector Opuesto o Negativo: es un vector que tiene la misma longitud y dirección pero en sentido contrario.
   

2. Vector Núlo o Cero: es aquel que tiene todos sus componentes iguales a cero. El vector nulo de R2 es O= (O,O). El vector nulo de R3 es (O,O,O).

3. Vector Columna: son vectores que se representan en forma de columna. 

   
   
   

4. Vector Fila o Reglón: Es el que está expresado en forma de fila. A= [1 2 3].
5. Vector Unitario: es aquel cuyo módulo o norma es igual a 1 (uno).

Módulo o Norma de un Vector:  Sea un Vector A la longitud de dicho vector se llama módulo o norma y se representa ||A||.

Teniendo un vector V= (X1,X2) el módulo se define de la siguiente manera ||V||= √(X1)2+(X2)2.

Puede ser expresado como V.V que es ||V||2 y por tanto esa doble raya es igual a la ||V||=√(V.V).

Propiedades de la Norma (Módulo).

Sea V un vector de Rn y K un escalar entonces:

1. ||V|| ≥ O, es decir que el módulo del vector debe ser positivo o igual a cero.
2. El módulo de K por la V es igual al valor absoluto de K veces la longitud de V  ||K.V||= |K| . ||V||.